Une présentation devrait intensifier la compréhension.
Je présente des chiffres sur le nombre d'indépendants par ville dans notre région, au fil du temps. Si au départ vous souhaiteriez avoir une définition plus précise de " travailleur indépendant," la voici.
Essayez d'observer comment vous réagissez à différentes façons de présenter ces données.
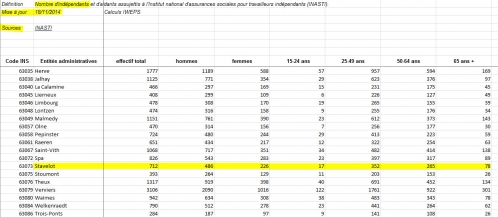
Ces données proviennent de l'INASTI (Institut national d'assurances sociales pour travailleurs indépendants) - voici leur tableur Excel des valeurs par ville pour toute la Wallonie (Stavelot est au numéro 63073). En cliquant sur ce lien, le fichier sera téléchargé sur vote ordinateur. Il vous faudra Excel pour l'ouvrir.
Présentation tableur : données brutes ...
- (cliquez sur l'image pour l'agrandir si besoin -
(Voici un lien pour mon tableau Excel pour ces valeurs et villes reprit dans l'article).
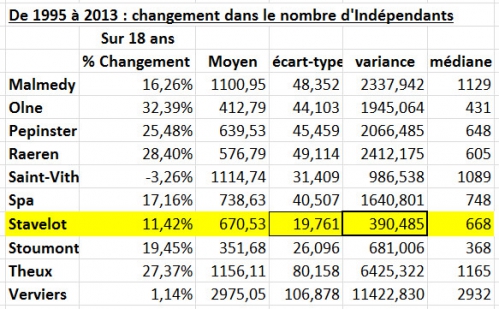
Un résumé mathématique des données à ce sujet :
Que dire ?
La moyenne nous donne une idée de la tendance centrale, avec le degré de variabilité autour de cette moyenne, représenté par l'écart-type et la variance. Ceux-ci permettent aussi de comparer deux moyennes avec d'autres outils statistiques, pour voir si ces moyennes sont identiques ou pas. La valeur médiane est la valeur "50 : 50" - pour Stavelot dans ces 18 années, 50% des valeurs étaient au dessus de 668, et dans l'autre moitié, en dessous de 668 indépendants. Le fait que la moyenne et la valeur médiane sont presque identiques veut dire qu'il n'y a pas beaucoup de valeurs abérrantes, aussi nommées "outliers" : une ou deux années très différentes de la valeur moyenne pour ces 18 ans, n'ont pas été découvertes.
(Si vous cherchez une revue efficace de ces termes provenant de la statistique descriptive, en voici une que vous pouvez sauvegarder).
La colonne "% Changement" représente le résultat de la dernière année (2013), moins la valeur dans la première année (1995), divisé par la première année (Donc, (712 - 639) / 639) ... une augmentation de 11,42% à Stavelot. Cette valeur divisée par les 18 années dans l'intervalle = 0,6344, un taux de croissance de 0,6% par année). En se servant de la variance pour comparer le nombre d'Indépendants dans ces villes, on peut voir rapidement que Stavelot à la valeur la plus basse. N'est-ce pas simplement un effet dû à des différences de population d'une ville à l'autre?
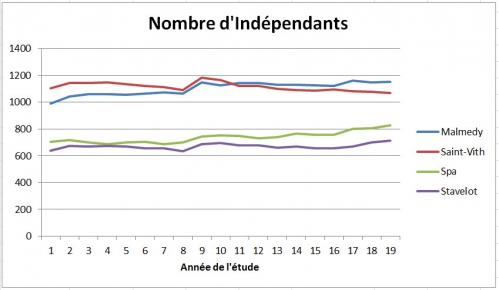
Réponse : Non, pas du tout, et que l'on vera un peu plus bas. Si l'on choisit 4 de ces villes pour les comparer, même un tableau comme celui-ci pourrait nous faire croire que c'est simplement une question de population, et que rien ne change à cours des années ...
Mais avant de quitter cet exemple, prenez un instant pour vous faire une idée de la facilité que vous avez eu pour extraire une comparaison utile pour vous, provenant des données dans ce résumé ci-dessus et ce graphique ...
Comment faire pour mesurer l'influence d'une chose sur une autre?
Même sans se permettre de dire qu'une chose est la cause d'une autre, voir comment une chose varie par rapport à une autre est fréquemment intéressant.
Nous avons mentionné la taille d'une ville comme peut-être déterminante du nombre d'indépendants que l'on y trouve. Regardons cela de plus près, en choisissant deux villes très connues ...
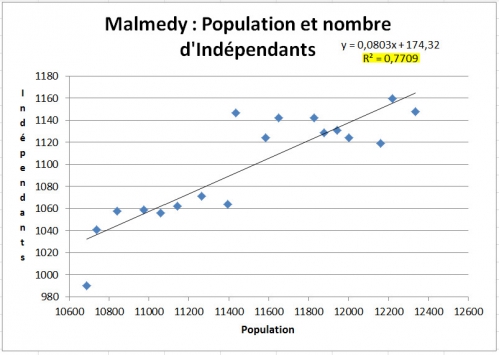
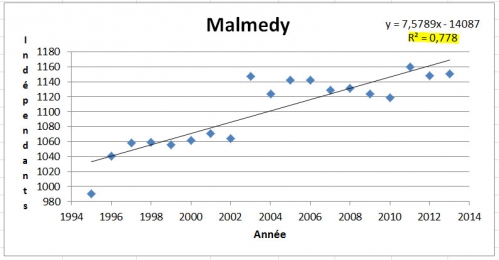
La population Malmédienne entre 1995 et 2012 sur l'axe horizontal, et le nombre d'indépendants dans les mêmes années. La ligne droite, qui est la meilleure ligne que l'on peut tirer pour marquer la relation entre ces points (ou losanges) a l'équation présenté à droite sur le haut du tableau. Mais à l'instant, décrivons ce qui est présenté juste en dessous de l'équation.
"R² = 0,7709"
C'est quoi ça? C'est un chiffre qui nous permet de comprendre la chose suivante : "Dans la variabilité perçue dans le nombre d'indépendants à Malmedy dans les années 1995 à 2012, quelle partie de cette variabilité semble d'être expliquée par la variabilité dans la population?" Et la réponse est la valeur du coéfficient de corrélation (R²), de 0,7709. Donc, les changements dans la population expliquent 77,1% de la variabilité observée dans le nombre d'indépendants. Ce chiffre est crée par le tableur basé sur l'équation de la ligne, mais qui donne une estimation très prudente. Calculé "à la main," la valeur est 0,87799, qui suggère que la population dans ces années étudiées, explique jusqu'à 87,8% de la variabilité perçue dans le nombre d'indépendants au travail à Malmedy.
Certains vont dire : "Bien sûr, et belle affaire ...
... plus il y a de personnes qui vivant dans une ville, plus il y aura d'indépendants pour les servir en gagnant leur vie."
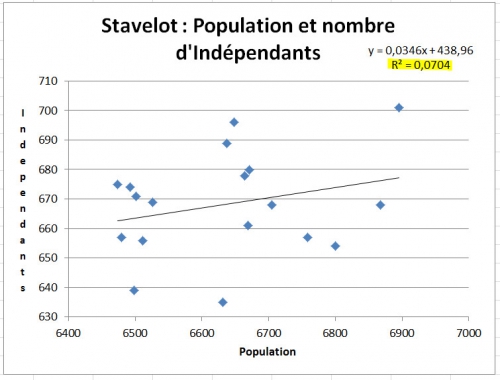
Mais, est-ce toujours vrai? Regardons les données pour ces mêmes années à Stavelot, avec la même forme de présentation :
En regardant ce graphique, on peut remarquer un certain nombre de choses :
- les points (ou losanges) sont plus dispersés
- ils ne suivent pas de près la ligne droite
- la ligne droite est plus horizontale, au lieu de monter du coin inférieur gauche vers le coin supérieur droit
- la valeur de R² est 0,0704, cela nous instruit que seulement 7,04% de la variabilité que l'on trouve dans le nombre d'indépendants au travail à Stavelot dans ces années ..., est expliquée par les chiffres de population. "Fait à la main" cette valeur donne R² = 0,265244 ou 26,5%.
Et de là, ce chiffre nous permet de dire que si on cherche à comprendre autant que possible, (disons à 100%) la variation dans le nombre d'independants à Stavelot entre 1995 et 2012, que 100 - 26,5 = 73,5% à 100 - 7,04 = 92,96% de ce mystère a son explication ailleurs que dans une relation avec la population de la ville dans les mêmes années.
Et quand, "Bien sûr," devient "Qui l'aurait pensé que ... ?"
... on commence à s'approcher moins de ce qu'on s'y attendait à trouver, et plus de ce qui est vraiment là, et en attente d'être trouvé.
Je vous laisse avec un autre exemple à parcourir comme exercice.
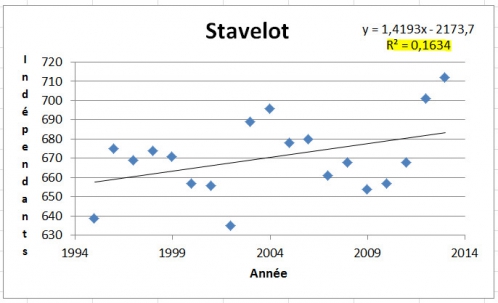
Est-ce que le nombre d'indépendants augmente simplement au cours des années? "Il y'en avait moins dans le passé, et il y'en aura plus demain ..."
Prenons les deux mêmes villes ...
Je vous donne un indice avec mon surligneur jaune :
L'exercice est offert pour souligner surtout que, la façon dont des informations sont présentées, détermine très souvent si le message est entendu ou non.
Bien que la corrélation n'implique pas forcément un lien de causalité, un essai contrôlé randomisé n'est pas toujours nécessaire, ni pratique, pour trouver un lien intéressant et souvant utile. Si variable "A" semble lié de très près aux changements dans le variable "B," il est aussi possible qu'un facteur à présent inconnu, "C," provoque les changements dans les deux autres. C'est souvant celui-là, "C," que l'on cherche.
Les gens qui boivent de l'eau finissent inévitablement morts. Donc cela suit que boire de l'eau provoque la mort.
Souvent, les données n'accordent pas facilement leurs secrets. Avez-vous une explication à partager pour les résultats observés pour les variations dans le nombre d'indépendants ?
Qui cherche, trouve, et celui qui ne cherche pas ...
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 6 autres membres